Previous topic
Using USim to solve 10 moment ions with 5 moment electrons
Next topic
Using USim to Solve Multi-Species Reactive Flows
Contents
Using USim to Solve Navier-Stokes Equations¶
Conservative form of Navier-Stokes equations are solved in USim. Convective and diffusion terms are de-coupled. Hence the diffusion terms are added as source in the Euler equations (see Using USim to solve the Euler Equations).
Contents
Viscous and Thermal Terms in Navier-Stokes Equations¶
Navier-Stokes equations are solved in Supersonic cross flow over cylinder example of the USimHS by adding the diffusion terms to regular Euler equations. The diffusion terms considered for the evaluation are found in navierStokesViscousOperator (1d, 2d, 3d). An example updater block that evaluates the diffusion terms in momentum and energy equations is shown below:
<Updater computeViscousFluxes>
kind = navierStokesViscousOperator2d
isRadial = false
numberOfInterpolationPoints = 8
onGrid = domain
coefficient = 1.0
enableThermal = true
enableViscous = true
temperatureIndex = 0
in = [velocity, dynamicViscosity, temperature, thermalCoefficient]
out = [source]
</Updater>
The meanings for the input blocks in this updater are as follows:
kind (string)
Specifies the navierStokesViscousOperator2d updater, which tells USim to evaluate the diffusion terms on two-dimensional grid. Similarly navierStokesViscousOperator1d and navierStokesViscousOperator3d can be used for one and three dimensional space domains.
isRadial (boolean)
Specifies whether the evaluation is carried out in cylindrical or Cartesian coordinates.
numberOfInterpolationPoints (string)
Number of interpolation points for leastsquares fit.
enableThermal (boolean)
Option to include heat conduction term in energy equation. time \(t\), here this is qSpecies.
enableViscous (boolean)
Option to include viscous terms in momentum and energy equations.
temperatureIndex (int)
Index of temperature in the array that stores temperature. Lets say the temperature array that is passed for diffusion source computation has three values translational, vibrational, and rotational temperature. Since translational temperature is used in the computation of heat conduction and viscous dissipation, we pass temperatureIndex = 0.
in (nodalArrays)
The variables required for the computation of diffusion terms. The names in the examples are self-explanatory and the order should not be changed.
out (nodalArray)
The variable to store the evluated diffusion terms.
Evaluation and Addition of the Diffusion Terms¶
The Updater block is evaluated in the time integration multiUpdater of the input file. Again referring to Supersonic cross flow over cylinder example of the USimHS package, the following updater block is used for time integration of fluxes using first order Runge-Kutta method. In this multiUpdater, computeViscousFluxes is added to the list of the updaters (updaters = [.,.,.,.,.]) to evaluate diffusion fluxes.:
<Updater rkUpdaterMain>
kind = multiUpdater2d
onGrid = domain
in = [q]
out = [qnew]
<TimeIntegrator rkIntegrator>
kind = rungeKutta2d
ongrid = domain
scheme = first
</TimeIntegrator>
<UpdateSequence sequence>
loop = [boundaries,compute,hyper]
</UpdateSequence>
<UpdateStep boundaries>
updaters = [correct, bcBottom, bcTop, bcRight, bcWall, bcLeft, computeT, bcWallTemp]
syncVars = [q]
</UpdateStep>
<UpdateStep compute>
operation = "operate"
updaters = [computeVelocity, computeViscosity, computeKinematicViscosity, computeThermalCoefficient, \
computeThermalDiffusivity, computeViscousFluxes]
syncVars = [source]
</UpdateStep>
<UpdateStep hyper>
operation = "integrate"
updaters = [hyper,addSource]
syncVars = [qnew]
</UpdateStep>
</Updater>
| option: | kind (string) |
|---|
name of of the this time integration updater multiUpdater2d (2d for two dimensional space).
| option: | in (nodalArray) variables to be integrated in time. |
|---|---|
| option: | out (nodalArray) name of the output variable. |
| option: | TimeIntegrator (sub block) type of integration scheme is rungeKutta2d with first order scheme. |
| option: | UpdateSequence (sub block) specifies the suquence loop of UpdateSteps. |
| option: | UpdateStep (sub blocks) Consists of the names of the user defined updater blocks required to be evaluated during the time integration steps. Note that, the names are user-given in the inputfile. And the order of evaluation is important. |
correct, bcBottom, bcTop, bcRight, bcWall, bcLeft, computeT, bcWallTemp, computeVelocity, computeViscosity, computeKinematicViscosity, computeThermalCoefficient, computeThermalDiffusivity, are the other updater blocks to evaluate and apply boundary conditions and thermophysical properties. These updater blocks are found in the Supersonic cross flow over cylinder example. Their usefulness will be briefed here in this lesson. correct corrects the values of any variables of interest to user specified limits. bcBottom, bcTop, bcRight, bcWall, bcLeft are the boundary conditions for conservative variables (here in this example, they are mass, three components of momentum, and energy density). computeT is for obtaining temperature from the conservative variables. bcWallTemp applies user specified temperature on the wall. ‘computeVelocity’ obtains the velocity from the conservative variables. computeViscosity, computeKinematicViscosity, computeThermalCoefficient, computeThermalDiffusivity are updater blocks used to compute thermophysical properties varying with temperature. Note that these blocks can be eliminated from the input file, if the properties are constant. computeViscousFluxes evaluates the viscous and thermal fluxes using the updater block shown above. hyper is classicMuscl updater block used to evaluate the convective fluxes from the hyperbolic part of the NS equations. Now the diffusion source is added to the existing convective sources using the combiner2d updater as shown below:
<Updater addSource>
kind = combiner2d
onGrid = domain
in = [qnew, source]
out = [qnew]
indVars_qnew = ["rho", "mx", "my", "mz", "en"]
indVars_source = ["sx","sy","sz","sen"]
exprs = ["rho","mx+sx","my+sy","mz+sz","en+sen"]
</Updater>
| option: | syncVars_computeViscousFluxes (optional attribute) This option synchronizes the diffusion fluxes in the variable source. All of the computed variables which need information from the cells in the adjacent partition (used in parallel computing) have to be synchronized using this option. Differentiation operators are used in computeViscousFluxes and the result is stored in source. Hence source is synChronized after calling computeViscousFluxes. |
|---|---|
| option: | syncVars_bcRight (optional attribute) used for the same reason as specified above. |
| option: | dummyVariables_q The dummy variables qDummy1, qDummy2, qDummy3 are required for Runge-Kutta integration. Each of the integration variable should have a different dummyVariables_ = [.,.,.] option. |
| option: | syncAfterSubStep qnew which has the updated values of the integration is synchronized at the end of integration. |
Time Step Restriction¶
Time step restriction has to be added separately for hyperbolic and elliptic terms. The following three restriction are evaluated and added in the loop.
Hyperbolic restriction:
<Updater timeStepRestriction>
kind = timeStepRestrictionUpdater2d
in = [q]
onGrid = domain
restrictions = [hyperbolic]
<TimeStepRestriction hyperbolic>
kind = hyperbolic
model = eulerEqn
cfl = CFL
gasGamma = GAS_GAMMA
</TimeStepRestriction>
</Updater>
Viscous diffusion time step restriction:
<Updater timeStepRestriction2>
kind = timeStepRestrictionUpdater2d
in = [kinematicViscosity]
onGrid = domain
restrictions = [quadratic]
<TimeStepRestriction quadratic>
kind = quadratic
cfl = 0.5
</TimeStepRestriction>
</Updater>
Thermal diffusion time step restriction:
<Updater timeStepRestriction3>
kind = timeStepRestrictionUpdater2d
in = [thermalDiffusivity]
onGrid = domain
restrictions = [quadratic]
<TimeStepRestriction quadratic>
kind = quadratic
cfl = 0.5
</TimeStepRestriction>
</Updater>
In all of the above time step restrictions, cfl can be varied according to the problem.
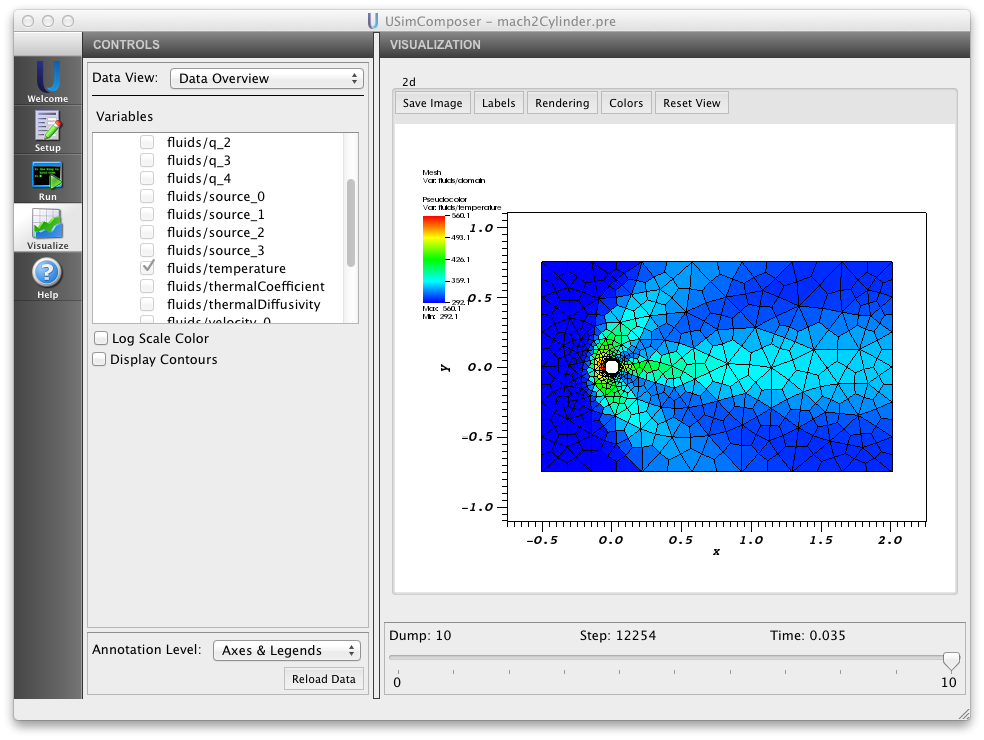
An Example Simulation¶
The Supersonic cross flow over cylinder example of the USimHS demonstrates each of the concepts described above. Executing the Supersonic cross flow over cylinder input file within USimComposer and switching to the Visualize tab yields the plot shown in Fig. 7.