Solving Multi-Dimensional Problems in USim¶
In Using USim to solve the Euler Equations we discussed the basic methods used by USim to solve the Euler equations. Next, in Using USim to solve the Magnetohydrodynamic Equations, we extended these ideas to solve the MHD equations in one-dimension and showed how USimBase simulations for both the Euler and MHD equations follow the same basic pattern. In this tutorial, we continue to build on these concepts and demonstrate how to use USim to solve the Euler and MHD equations in multi-dimensions, how to utilize more advanced boundary conditions and how to apply external fources (such as gravity) to the equations.
This tutorial is based on Rayleigh-Taylor Instability (rtInstability.pre) in USimBase, which demonstrates the well-known Rayleigh-Taylor instability problem described by:
Jun, Norman, & Stone, ApJ 453, 332 (1995).
Contents
Initializing the Simulation¶
Compared to the ShockTube example used in Using USim to solve the Euler Equations, the initialization of the simulation proceeds in a similar fashion, with parameters customized for the Rayleigh-Taylor problem:
# Import macros to setup simulation
$ import fluidsBase.mac
$ import euler.mac
# X-extent of domain
$ PAR_LENGTH = 1.5
# Y-extent of domain
$ TRANS_LENGTH = 0.5
# Zones parallel to shear direction
$ PAR_ZONES = 192
# Zones perpendicular to shear direction
$ TRANS_ZONES = 64
# adiabatic index
$ GAS_GAMMA = 1.4
# acceleration due to gravity
$ GRAVITY_ACCEL = 0.1
# Upper fluid density
$ RHO_HEAVY = 2.0
# Lower fluid density
$ RHO_LIGHT = 1.0
# Magnetic field strength
$ BETA = 1.0e3
# Amplitude of perturbation
$ PERTURB_AMP = 0.01
# end time for simulation
$ TEND = 12.75
# number of frames
$ NUMDUMPS = 10
# Whether to use diffusive (but robust) fluxes
$ DIFFUSIVE = False
# Order in time
$ TIME_ORDER = "second"
# Write data for restarting the simulation
$ WRITE_RESTART = False
# Output info for debugging purposes
$ DEBUG = False
# Default dimensionality
$ NDIM = 2
# Initialize a USim simulation
initializeFluidSimulation(NDIM,0.0,TEND,NUMDUMPS,CFL,GAS_GAMMA,WRITE_RESTART,DEBUG)
Adding a Simulation Grid¶
Compared to the ShockTube example used in Using USim to solve the Euler Equations, adding a grid again proceeds in a similar fashion, with parameters customized for the Rayleigh-Taylor problem:
$XMIN = -0.5*TRANS_LENGTH
$XMAX = 0.5*TRANS_LENGTH
$YMIN = -0.5*PAR_LENGTH
$YMAX = 0.5*PAR_LENGTH
$ZMIN = -0.5*TRANS_LENGTH
$ZMAX = 0.5*TRANS_LENGTH
$if NDIM==2
$ CFL = 0.4
$ numCells = [TRANS_ZONES, PAR_ZONES]
$ periodicDirections = [0]
$ lowerBounds = [XMIN, YMIN]
$ upperBounds = [XMAX, YMAX]
$ else
$ CFL = 0.32
$ numCells = [TRANS_ZONES, PAR_ZONES, TRANS_ZONES]
$ periodicDirections = [0 2]
$ lowerBounds = [XMIN, YMIN, ZMIN]
$ upperBounds = [XMAX, YMAX, ZMAX]
$ endif
addGrid(lowerBounds, upperBounds, numCells, periodicDirections)
Note that directions 0 (x) and (in three-dimensions) 2 (z) are periodic. Our simulation now looks like:
# Import macros to setup simulation
$ import fluidsBase.mac
$ import euler.mac
# X-extent of domain
$ PAR_LENGTH = 1.5
# Y-extent of domain
$ TRANS_LENGTH = 0.5
# Zones parallel to shear direction
$ PAR_ZONES = 192
# Zones perpendicular to shear direction
$ TRANS_ZONES = 64
# adiabatic index
$ GAS_GAMMA = 1.4
# acceleration due to gravity
$ GRAVITY_ACCEL = 0.1
# Upper fluid density
$ RHO_HEAVY = 2.0
# Lower fluid density
$ RHO_LIGHT = 1.0
# Magnetic field strength
$ BETA = 1.0e3
# Amplitude of perturbation
$ PERTURB_AMP = 0.01
# end time for simulation
$ TEND = 12.75
# number of frames
$ NUMDUMPS = 10
# Whether to use diffusive (but robust) fluxes
$ DIFFUSIVE = False
# Order in time
$ TIME_ORDER = "second"
# Write data for restarting the simulation
$ WRITE_RESTART = False
# Output info for debugging purposes
$ DEBUG = False
# Default dimensionality
$ NDIM = 2
$XMIN = -0.5*TRANS_LENGTH
$XMAX = 0.5*TRANS_LENGTH
$YMIN = -0.5*PAR_LENGTH
$YMAX = 0.5*PAR_LENGTH
$ZMIN = -0.5*TRANS_LENGTH
$ZMAX = 0.5*TRANS_LENGTH
$if NDIM==2
$ CFL = 0.4
$ numCells = [TRANS_ZONES, PAR_ZONES]
$ periodicDirections = [0]
$ lowerBounds = [XMIN, YMIN]
$ upperBounds = [XMAX, YMAX]
$ else
$ CFL = 0.32
$ numCells = [TRANS_ZONES, PAR_ZONES, TRANS_ZONES]
$ periodicDirections = [0 2]
$ lowerBounds = [XMIN, YMIN, ZMIN]
$ upperBounds = [XMAX, YMAX, ZMAX]
$ endif
# Initialize a USim simulation
initializeFluidSimulation(NDIM,0.0,TEND,NUMDUMPS,CFL,GAS_GAMMA,WRITE_RESTART,DEBUG)
# Setup the grid
addGrid(lowerBounds, upperBounds, numCells, periodicDirections)
Creating a Fluid Simulation¶
This initial condition for this problem is hydrostatic equilibrium consisting of a heavier fluid supported by a lighter fluid, which is perturbed with a single mode. Initialization follows the same pattern as in Using USim to solve the Euler Equations. First, we create the variables needed to simulate the fluid:
createFluidSimulation()
We then proceed through the three-step process to specify the distribution of the fluid on the grid. Step 1: Add Variables:
addVariable(gas_gamma,GAS_GAMMA)
addVariable(rhoTop,RHO_HEAVY)
addVariable(rhoBottom,RHO_LIGHT)
addVariable(perturb,PERTURB_AMP)
addVariable(ytop,YMAX)
addVariable(gravity,GRAVITY_ACCEL)
addVariable(lx,TRANS_LENGTH)
addVariable(ly,PAR_LENGTH)
Step 2: Add Pre Expression’s:
addPreExpression(p0 = 0.01)
addPreExpression(pert = 0.01)
addPreExpression(pi = 3.14159)
addPreExpression(rho = if (y < 0.0, rhoBottom, rhoTop))
addPreExpression(pr = (1.0/gas_gamma) - (gravity*rho*y))
addPreExpression(vx = 0.0)
addPreExpression(vy = (0.25*perturb)*(1.0 + cos(2.0*pi*x/lx))*(1.0 + cos(2.0*pi*y/ly)))
addPreExpression(vz = 0.0)
Step 3: Add Expressions for density, momentum and total energy:
addExpression(rho)
addExpression(rho*vx)
addExpression(rho*vy)
addExpression(rho*vz)
addExpression((pr/(gas_gamma-1.0))+0.5*rho*(vx*vx+vy*vy+vz*vz))
Note that Step 3 is identical to that used in Using USim to solve the Euler Equations. Our simulation now looks like:
# Import macros to setup simulation
$ import fluidsBase.mac
$ import euler.mac
# X-extent of domain
$ PAR_LENGTH = 1.5
# Y-extent of domain
$ TRANS_LENGTH = 0.5
# Zones parallel to shear direction
$ PAR_ZONES = 192
# Zones perpendicular to shear direction
$ TRANS_ZONES = 64
# adiabatic index
$ GAS_GAMMA = 1.4
# acceleration due to gravity
$ GRAVITY_ACCEL = 0.1
# Upper fluid density
$ RHO_HEAVY = 2.0
# Lower fluid density
$ RHO_LIGHT = 1.0
# Magnetic field strength
$ BETA = 1.0e3
# Amplitude of perturbation
$ PERTURB_AMP = 0.01
# end time for simulation
$ TEND = 12.75
# number of frames
$ NUMDUMPS = 10
# Whether to use diffusive (but robust) fluxes
$ DIFFUSIVE = False
# Order in time
$ TIME_ORDER = "second"
# Write data for restarting the simulation
$ WRITE_RESTART = False
# Output info for debugging purposes
$ DEBUG = False
# Default dimensionality
$ NDIM = 2
$XMIN = -0.5*TRANS_LENGTH
$XMAX = 0.5*TRANS_LENGTH
$YMIN = -0.5*PAR_LENGTH
$YMAX = 0.5*PAR_LENGTH
$ZMIN = -0.5*TRANS_LENGTH
$ZMAX = 0.5*TRANS_LENGTH
$if NDIM==2
$ CFL = 0.4
$ numCells = [TRANS_ZONES, PAR_ZONES]
$ periodicDirections = [0]
$ lowerBounds = [XMIN, YMIN]
$ upperBounds = [XMAX, YMAX]
$ else
$ CFL = 0.32
$ numCells = [TRANS_ZONES, PAR_ZONES, TRANS_ZONES]
$ periodicDirections = [0 2]
$ lowerBounds = [XMIN, YMIN, ZMIN]
$ upperBounds = [XMAX, YMAX, ZMAX]
$ endif
# Initialize a USim simulation
initializeFluidSimulation(NDIM,0.0,TEND,NUMDUMPS,CFL,GAS_GAMMA,WRITE_RESTART,DEBUG)
# Setup the grid
addGrid(lowerBounds, upperBounds, numCells, periodicDirections)
# Create data structures needed for the simulation
createFluidSimulation()
# Step 1: Add Variables
addVariable(gas_gamma,GAS_GAMMA)
addVariable(rhoTop,RHO_HEAVY)
addVariable(rhoBottom,RHO_LIGHT)
addVariable(perturb,PERTURB_AMP)
addVariable(ytop,YMAX)
addVariable(gravity,GRAVITY_ACCEL)
addVariable(lx,TRANS_LENGTH)
addVariable(ly,PAR_LENGTH)
# Step 2: Add Pre-Expressions
addPreExpression(p0 = 0.01)
addPreExpression(pert = 0.01)
addPreExpression(pi = 3.14159)
addPreExpression(rho = if (y < 0.0, rhoBottom, rhoTop))
addPreExpression(pr = (1.0/gas_gamma) - (gravity*rho*y))
addPreExpression(vx = 0.0)
addPreExpression(vy = (0.25*perturb)*(1.0 + cos(2.0*pi*x/lx))*(1.0 + cos(2.0*pi*y/ly)))
addPreExpression(vz = 0.0)
# Step 3: Add expressions specifying initial condition on density,
# momentum, total energy
addExpression(rho)
addExpression(rho*vx)
addExpression(rho*vy)
addExpression(rho*vz)
addExpression((pr/(gas_gamma-1))+0.5*rho*(vx*vx+vy*vy+vz*vz))
Compared to the simulation described in Using USim to solve the Euler Equations, the similarities should be obvious as the simulation is following the pattern:
# Specify parameters for the specific physics problem
$ PARAM_1 = <value>
$ PARAM_2 = <value>
$ PARAM_N = <value>
# Initialize a USim simulation
initializeFluidSimulation(NDIM,0.0,END_TIME,NUMDUMPS,CFL,GAS_GAMMA,WRITE_RESTART,DEBUG)
# Setup the grid
addGrid(lowerBounds, upperBounds, numCells, periodicDirections)
# Create data structures needed for the simulation
createFluidSimulation()
# Specify initial condition
# Step 1: Add Variables
addVariable(NAME,<value>)
# Step 2: Add Pre-Expressions
addPreExpression(<PreExpression>)
# Step 3: Add expressions specifying initial condition on density,
# momentum, total energy
addExpression(<expression>)
Evolving the Fluid¶
There are two major differences in simulating the Rayleigh-Taylor problem compared to a shock tube: acceleration due to gravity and boundary conditions. These change the scheme for integrating the hyperbolic conservation law, which now looks like:
#
# Add the spatial discretization of the fluxes
finiteVolumeScheme(DIFFUSIVE)
#
# Add source term for gravitational acceleration to the equations
addGravitationalAcceleration(GRAVITY_ACCEL)
#
# Boundary conditions
boundaryCondition(wall,top)
boundaryCondition(wall,bottom)
boundaryCondition(periodic)
#
# Time integration
timeAdvance(TIME_ORDER)
The first major difference is the addition of a gravitational acceleration. This is done through a simple macro call after we have defined the finiteVolumeScheme:
addGravitationalAcceleration(GRAVITY_ACCEL)
The next is that we add wall or reflecting boundary conditions at the top and bottom of the grid. These boundary conditions are documented at eulerBc (1d, 2d, 3d):
boundaryCondition(wall,top)
boundaryCondition(wall,bottom)
Putting it all Together¶
As before, the final step in the USim simulation is to add:
runFluidSimulation()
So, our simulation now looks like:
# Import macros to setup simulation
$ import fluidsBase.mac
$ import euler.mac
# X-extent of domain
$ PAR_LENGTH = 1.5
# Y-extent of domain
$ TRANS_LENGTH = 0.5
# Zones parallel to shear direction
$ PAR_ZONES = 192
# Zones perpendicular to shear direction
$ TRANS_ZONES = 64
# adiabatic index
$ GAS_GAMMA = 1.4
# acceleration due to gravity
$ GRAVITY_ACCEL = 0.1
# Upper fluid density
$ RHO_HEAVY = 2.0
# Lower fluid density
$ RHO_LIGHT = 1.0
# Magnetic field strength
$ BETA = 1.0e3
# Amplitude of perturbation
$ PERTURB_AMP = 0.01
# end time for simulation
$ TEND = 12.75
# number of frames
$ NUMDUMPS = 10
# Whether to use diffusive (but robust) fluxes
$ DIFFUSIVE = False
# Order in time
$ TIME_ORDER = "second"
# Write data for restarting the simulation
$ WRITE_RESTART = False
# Output info for debugging purposes
$ DEBUG = False
# Default dimensionality
$ NDIM = 2
$XMIN = -0.5*TRANS_LENGTH
$XMAX = 0.5*TRANS_LENGTH
$YMIN = -0.5*PAR_LENGTH
$YMAX = 0.5*PAR_LENGTH
$ZMIN = -0.5*TRANS_LENGTH
$ZMAX = 0.5*TRANS_LENGTH
$if NDIM==2
$ CFL = 0.4
$ numCells = [TRANS_ZONES, PAR_ZONES]
$ periodicDirections = [0]
$ lowerBounds = [XMIN, YMIN]
$ upperBounds = [XMAX, YMAX]
$ else
$ CFL = 0.32
$ numCells = [TRANS_ZONES, PAR_ZONES, TRANS_ZONES]
$ periodicDirections = [0 2]
$ lowerBounds = [XMIN, YMIN, ZMIN]
$ upperBounds = [XMAX, YMAX, ZMAX]
$ endif
# Initialize a USim simulation
initializeFluidSimulation(NDIM,0.0,TEND,NUMDUMPS,CFL,GAS_GAMMA,WRITE_RESTART,DEBUG)
# Setup the grid
addGrid(lowerBounds, upperBounds, numCells, periodicDirections)
# Create data structures needed for the simulation
createFluidSimulation()
# Step 1: Add Variables
addVariable(gas_gamma,GAS_GAMMA)
addVariable(rhoTop,RHO_HEAVY)
addVariable(rhoBottom,RHO_LIGHT)
addVariable(perturb,PERTURB_AMP)
addVariable(ytop,YMAX)
addVariable(gravity,GRAVITY_ACCEL)
addVariable(lx,TRANS_LENGTH)
addVariable(ly,PAR_LENGTH)
# Step 2: Add Pre-Expressions
addPreExpression(p0 = 0.01)
addPreExpression(pert = 0.01)
addPreExpression(pi = 3.14159)
addPreExpression(rho = if (y < 0.0, rhoBottom, rhoTop))
addPreExpression(pr = (1.0/gas_gamma) - (gravity*rho*y))
addPreExpression(vx = 0.0)
addPreExpression(vy = (0.25*perturb)*(1.0 + cos(2.0*pi*x/lx))*(1.0 + cos(2.0*pi*y/ly)))
addPreExpression(vz = 0.0)
# Step 3: Add expressions specifying initial condition on density,
# momentum, total energy
addExpression(rho)
addExpression(rho*vx)
addExpression(rho*vy)
addExpression(rho*vz)
addExpression((pr/(gas_gamma-1))+0.5*rho*(vx*vx+vy*vy+vz*vz))
# Add the spatial discretization of the fluxes
finiteVolumeScheme(DIFFUSIVE)
# Add source term for gravitational acceleration to the equations
addGravitationalAcceleration(GRAVITY_ACCEL)
# Boundary conditions
boundaryCondition(wall,top)
boundaryCondition(wall,bottom)
boundaryCondition(periodic)
# Time integration
timeAdvance(TIME_ORDER)
# Run the simulation!
runFluidSimulation()
Note
For more depth, you can view the actual input blocks to Ulixes in the Setup window by choosing Save And Process Setup and then clicking on the shockTube.in file. In the .in file all macros are expanded to produce input blocks.
Solving the MHD Equations in Multi-Dimensions¶
We can extend the approach above to solving the MHD equations in multi-dimensions in a straightforward fashion. The steps for Creating a Fluid Simulation is unchanged from Using USim to solve the Magnetohydrodynamic Equations, while the steps for Adding a Simulation Grid are identical to that given above. The differences come in Creating a Fluid Simulation, where Steps 1) - 3) of specifying the initial condition change:
Step 1: Add Variables:
addVariable(gas_gamma,GAS_GAMMA)
addVariable(rhoTop,RHO_HEAVY)
addVariable(rhoBottom,RHO_LIGHT)
addVariable(perturb,PERTURB_AMP)
addVariable(ytop,YMAX)
addVariable(gravity,GRAVITY_ACCEL)
addVariable(lx,TRANS_LENGTH)
addVariable(ly,PAR_LENGTH)
addVariable(mu0,MU0)
addVariable(beta,BETA)
Step 2: Add Pre Expression’s:
addPreExpression(p0 = 0.01)
addPreExpression(pert = 0.01)
addPreExpression(pi = 3.14159)
addPreExpression(rho = if (y < 0.0, rhoBottom, rhoTop))
addPreExpression(pr = (1.0/gas_gamma) - (gravity*rho*y))
addPreExpression(vx = 0.0)
addPreExpression(vy = (0.25*perturb)*(1.0 + cos(2.0*pi*x/lx))*(1.0 + cos(2.0*pi*y/ly)))
addPreExpression(vz = 0.0)
addPreExpression(bx = sqrt(2.0*pr/(beta*beta)))
addPreExpression(by = 0.0)
addPreExpression(bz = 0.0)
addPreExpression(psi = 0.0)
Step 3: Add Expressions for density, momentum, total energy, magnetic field and correction potential:
addExpression(rho)
addExpression(rho*vx)
addExpression(rho*vy)
addExpression(rho*vz)
addExpression(pr/(gas_gamma-1.0) + 0.5*rho*(vy*vy)+0.5*((bx*bx)/mu0))
addExpression(bx)
addExpression(by)
addExpression(bz)
addExpression(psi)
The remaining steps in setting up the simulation are unchanged. We can then extend the underlying pattern for USimBase simulations:
# Are we solving the MHD equations?
$ MHD = True
# Import macros to setup simulation
$ import fluidsBase.mac
# if MHD
$ import idealmhd.mac
$ else
$ import euler.mac
$ endif
# Specify parameters for the specific physics problem
$ PARAM_1 = <value>
$ PARAM_2 = <value>
$ PARAM_N = <value>
# Initialize a USim simulation
$ if MHD
initializeFluidSimulation(NDIM,0.0,END_TIME,NUMDUMPS,CFL,GAS_GAMMA,MU0,WRITE_RESTART,DEBUG)
$ else
initializeFluidSimulation(NDIM,0.0,END_TIME,NUMDUMPS,CFL,GAS_GAMMA,WRITE_RESTART,DEBUG)
$ endif
# Setup the grid
addGrid(lowerBounds, upperBounds, numCells, periodicDirections)
# Create data structures needed for the simulation
createFluidSimulation()
# Specify initial condition
# Step 1: Add Variables
addVariable(NAME,<value>)
# Step 2: Add Pre-Expressions
addPreExpression(<PreExpression>)
# Step 3: a) Add expressions specifying initial condition on density,
# momentum
addExpression(<expression>)
$ if MHD
# Step 3: b) Add expression specifying initial conditions on total
# energy, magnetic field, correction potential
addExpression(<expression>)
$ else
# Step 3: b) Add expression specifying initial conditions on total
# energy
addExpression(<expression>)
$ endif
# Add the spatial discretization of the fluxes
finiteVolumeScheme(DIFFUSIVE)
# Add (optional) physics to the finite volume scheme
< physics macros >
# Boundary conditions
boundaryCondition(<boundaryCondition,entity>)
# Time integration
timeAdvance(TIME_ORDER)
# Run the simulation!
runFluidSimulation()
Note
The algorithms in USim automatically preserve \(\nabla \cdot B = 0\) (the solenoidal constraint on the magnetic field), so there is no need for the user to make changes to the algorithm at the input file level when running in multi-dimensions.
An Example Simulation¶
The input file for the problem Rayleigh-Taylor Instability in the USimBase package demonstrates each of the concepts described above to evolve the Rayleigh-Taylor instability for a single mode perturbation. An additional example of these concepts can be found in the Kelvin-Helmholtz Instability input file in the USimBase package.
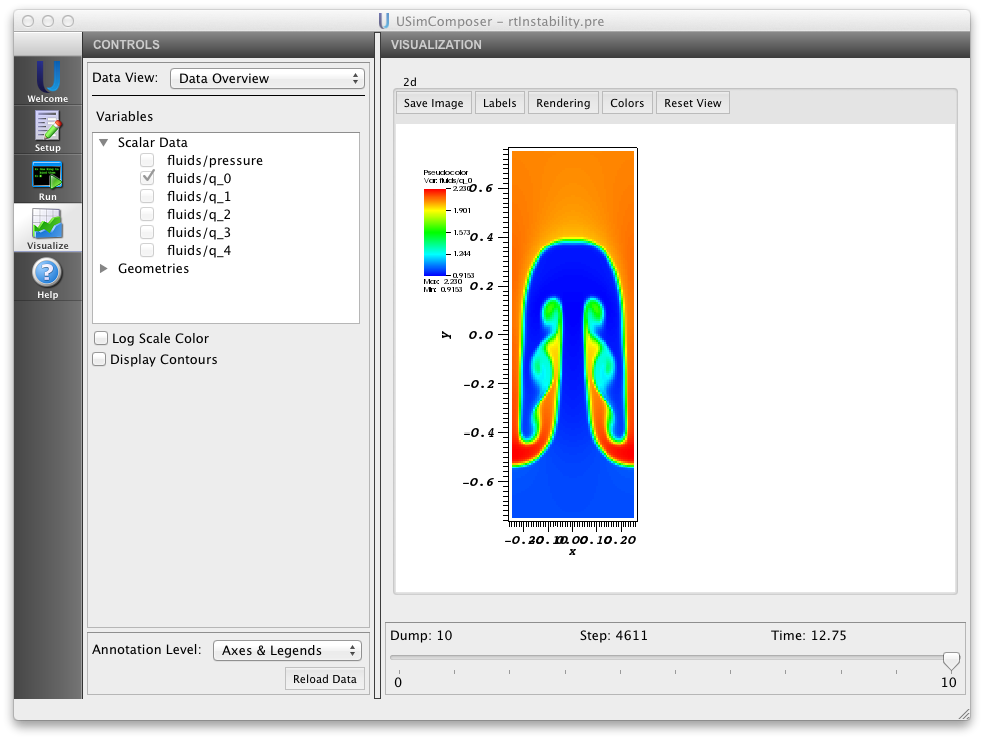
Executing the Rayleigh-Taylor input file within USimComposer and switching to the Visualize tab yields the plots shown in Fig. 2.
Note that it is possible to execute both the Rayleigh-Taylor Instability and Kelvin-Helmholtz Instability examples in the USimBase package using MHD by selecting MHD = True.