Using USim to solve the Euler Equations

In this tutorial, we demonstrate the basic methods used by USim to solve the Euler equations. This will serve as a foundation for understanding how to run any simulation in USim.

The Euler Equations

This tutorial is based on the Shock Tube (shockTube.pre) example. The Shock Tube simulation is designed to set up a variety of tube simulations including those by Einfeldt, Sod, Liska & Wendroff, Brio & Wu, and Ryu & Jones. In this tutorial, we will look at the Sod Shock Tube based on the classic paper:

Sod, Gary A. "A survey of several finite difference methods for
systems of nonlinear hyperbolic conservation laws.";
Journal of Computational Physics 27.1 (1978): 1-31.

Note

It is important to note that while we will be following the Shock Tube (shockTube.pre) example, we will not reproduce the example file in its entirety. The shockTube example is designed to set up a variety of simulations, and by using “Flags” (if statements) in the shockTube.pre file, only certain parts of the file are used when simulating the Sod Shock Tube. Therefore, at the end of this tutorial, our input will not be an exact copy of the shockTube.pre file but will directly represent only the Sod Shock portion of it.

In this example we will look at the use of equations for inviscid compressible hydrodynamics (the Euler equations). It is appropriate to use these equations for transonic, supersonic and hypersonic flows (Mach numbers of 0.1 and above) where compressibility effects are important and at high Reynolds numbers where the effects of viscosity and conductivity are relatively unimportant.

The Euler equations for an adiabatic gas can be written as a hyperbolic conservation law, which has the form:

\[\notag \begin{align} \frac{\partial \mathbf{q}}{\partial t} + \nabla\cdot\left[ \mathcal{F} \left( \mathbf{w} \right) \right] = 0 \end{align}\]

where \(\mathbf{q}\) is a vector of conserved variables (e.g. density, momentum, total energy), \(\mathcal{F}\left( \mathbf{w} \right)\) is a non-linear flux tensor computed from a vector of primitive variables, (e.g. density, velocity, pressure), and \(\mathbf{w} = \mathbf{w}(\mathbf{q})\). Assuming an adiabatic equations of state, the Euler equations can be written in this form such that:

\[\notag \begin{align} \frac{\partial \rho}{\partial t} + \nabla\cdot\left[ \rho\,\mathbf{u} \right] = 0 \\ \frac{\partial \rho\,\mathbf{u}}{\partial t} + \nabla\cdot\left[ \rho\,\mathbf{u}\,\mathbf{u}^{T} + \mathbb{I} P \right] = 0 \\ \frac{\partial E}{\partial t} + \nabla\cdot\left[ \left(E + P \right) \mathbf{u} \right] = 0 \end{align}\]

Here, \(\mathbb{I}\) is the identity matrix, \(P = \rho\epsilon(\gamma-1)\) is the pressure of an ideal gas, \(\epsilon\) is the specific internal energy and \(\gamma\) is the adiabatic index (ratio of specific heats).

The Euler equations are represented in USim by eulerEqn. USim solves these equations by calculating an upwind approximation of the flux tensor, \(\mathcal{F}(\mathbf{w})\) (see classicMusclUpdater (1d, 2d, 3d)) and then using this approximation to advance the conserved state from time \(t\) to \(t+\Delta t\) (see multiUpdater (1d, 2d, 3d)).

In this tutorial, we introduce the structure of a USim simulation, using Shock Tube (shockTube.pre) as an example. At the end of this tutorial, you will understand how to setup simple USim simulations on structured meshes.

Initializing a Simulation

The first step in any USim simulation is to import the macros that are needed to define the simulation. For the ShockTube example, there are two macros that are needed:

$ import fluidsBase.mac
$ import euler.mac

These macros provide basic capabilities for setting up a USim simulation of the Euler Equations. We can now define global parameters that tell USim basic information about the simulation. This is done through the use of the initializeFluidSimulation macro:

initializeFluidSimulation(NDIM,0.0,END_TIME,NUMDUMPS,CFL,GAS_GAMMA,WRITE_RESTART,DEBUG)

The parameters for the version of the macro used for the eulerEqn are documented at Euler Macro. For completeness, we include them here, showing how the parameters specified here map onto the parameters used in the initializeFluidSimulation macro:

NDIM (dimensionality):
1,2,3. Number of dimensions for the simulation
0.0 (tStart):
Start time for simulation
END_TIME (tEnd):
End time for simulation
NUMDUMPS (numFrames):
Number of data outputs
CFL (cflNum):
Cfl limit, typically \(\Delta t = cflNum * \Delta x / V_{max}\)
GAS_GAMMA (gammaIn):
Adiabatic index for ideal gas eqn. of state. Pressure = (gammaIn - 1.0) * density * internal energy
WRITE_RESTART (writeRestartIn):
Output data required for simulation restart
DEBUG (debugIn):
Run simulation in debug mode

USim includes the ability to perform in place substitution of variables within the input file, as described in Symbol Definition. This means that we can define the options given above earlier in the input file and USim will replace them in the initializeFluidSimulation macro:

# X-extent of domain
$PAR_LENGTH = 1.0
# Y-extent of domain
$PERP_LENGTH = 1.0
# Zones parallel to shock normal direction
$PAR_ZONES = 256
# Zones perpendicular to shock normal direction
$PERP_ZONES = 256
# Shock tube to solve
$SHOCK_TUBE = "SOD"
# adiabatic index
$GAS_GAMMA = 5.0/3.0
# Atmospheric Pressure
$REFERENCE_PRESSURE = 1.0 # [Pa]
# density of air
$REFERENCE_DENSITY = 1.0 # [kg/m^3]
# end time for simulation (units of # of sound wave crossings)
$TEND = 0.125
# number of frames
$NUMDUMPS = 10
# Whether to use a diffusive (but robust) integration scheme
$DIFFUSIVE = False
# Order in time
$TIME_ORDER = "second"
# Write data for restarting the simulation
$WRITE_RESTART = False
# Output info for debugging purposes
$DEBUG = False
# Default dimensionality
$NDIM = 1

Note that we have included a range of other variables that are defined in the Shock Tube (shockTube.pre) example. We will refer to these later in this tutorial as needed. In the above, the variable TEND is given in units of the the number of times a sound wave crosses the grid. In order to use this to specify the end time for the simulation (END_TIME), we convert this to have units of time through:

# nominal speed of sound
$ c0 = math.sqrt(GAS_GAMMA*REFERENCE_PRESSURE/REFERENCE_DENSITY) # [m/s]

# Set end time according to (user specified)
# number of times a wave crosses the box.
$END_TIME = $PERP_LENGTH*TEND/c0$

The specification of the CFL parameter is described in the next section. Our simulation starts off as:

# Import macros to setup simulation
$ import fluidsBase.mac
$ import euler.mac

# X-extent of domain
$PAR_LENGTH = 1.0
# Y-extent of domain
$PERP_LENGTH = 1.0
# Zones parallel to shock normal direction
$PAR_ZONES = 256
# Zones perpendicular to shock normal direction
$PERP_ZONES = 256
# Shock tube to solve
$SHOCK_TUBE = "SOD"
# adiabatic index
$GAS_GAMMA = 5.0/3.0
# Atmospheric Pressure
$REFERENCE_PRESSURE = 1.0 # [Pa]
# density of air
$REFERENCE_DENSITY = 1.0 # [kg/m^3]
# end time for simulation (units of # of sound wave crossings)
$TEND = 0.125
# number of frames
$NUMDUMPS = 10
# Whether to use a diffusive (but robust) integration scheme
$DIFFUSIVE = False
# Order in time
$TIME_ORDER = "second"
# Write data for restarting the simulation
$WRITE_RESTART = False
# Output info for debugging purposes
$DEBUG = False
# Default dimensionality
$NDIM = 1

# nominal speed of sound
$ c0 = math.sqrt(GAS_GAMMA*REFERENCE_PRESSURE/REFERENCE_DENSITY) # [m/s]

# Set end time according to (user specified)
# number of times a wave crosses the box.
$END_TIME = $PERP_LENGTH*TEND/c0$

# Initialize a USim simulation
initializeFluidSimulation(NDIM,0.0,END_TIME,NUMDUMPS,CFL,GAS_GAMMA,WRITE_RESTART,DEBUG)

Adding a Simulation Grid

The next step in setting up a USim simulation is to specify a simulation grid. The Shock Tube (shockTube.pre) uses a cart (1d, 2d, 3d) grid, which is added to the simulation through the addGrid macro:

addGrid(lowerBounds, upperBounds, numCells, periodicDirections)

The options for this macro are documented in Grid Macro. For completeness, we include them here:

lowerBounds:
Vector of coordinates for lower edge of grid, lowerBounds = [ XMIN YMIN ZMIN ]
upperBounds:
Vector of coordinates for upper edge of grid, upperBounds = [ XMAX YMAX ZMAX ]
numCells:
Vector of number of cells in grid, numCells = [ NX NY NZ ]
periodicDirections:

List of directions that are periodic

periodicDirections = [ 0 ] (x-direction periodic)
periodicDirections = [ 0 1 ] (x,y-directions periodic)
periodicDirections = [ 0 1 2 ] (x,y,z-directions periodic)

The options are setup in the ShockTube example according to the dimensionality of the simulation, as specified by the variable NDIM above:

$XMIN = -0.5*PERP_LENGTH
$XMAX =  0.5*PERP_LENGTH
$YMIN = -0.5*PAR_LENGTH
$YMAX =  0.5*PAR_LENGTH
$ZMIN = -0.5*PAR_LENGTH
$ZMAX =  0.5*PAR_LENGTH

$if NDIM==1
$ CFL = 0.5
$ numCells = [PERP_ZONES]
$ periodicDirections = []
$ lowerBounds = [XMIN]
$ upperBounds = [XMAX]
$ else
$if NDIM==2
$ CFL = 0.4
$ numCells = [PERP_ZONES, PAR_ZONES]
# Make the direction perpendicular to the shock
# normal periodic.
$ periodicDirections = [1]
$ lowerBounds = [XMIN,  YMIN]
$ upperBounds = [XMAX,  YMAX]
$ else
$ CFL = 0.32
$ numCells = [PERP_ZONES, PAR_ZONES, PAR_ZONES]
# Make the directions perpendicular to the shock
# normal periodic.
$ periodicDirections = [1,2]
$ lowerBounds = [XMIN,  YMIN,  ZMIN]
$ upperBounds = [XMAX,  YMAX,  ZMAX]
$ endif
$ endif

Note as well that the CFL condition that is used for the simulation changes according to the dimension of the simulation. This is because the scheme for solving the hyperbolic equations has different stability requirements in different dimensions:

\[\notag \begin{align} \mathrm{CFL} <= \frac{1}{\mathrm{NDIM}} \end{align}\]

So, our simulation now looks like:

# Import macros to setup simulation
$ import fluidsBase.mac
$ import euler.mac

# X-extent of domain
$PAR_LENGTH = 1.0
# Y-extent of domain
$PERP_LENGTH = 1.0
# Zones parallel to shock normal direction
$PAR_ZONES = 256
# Zones perpendicular to shock normal direction
$PERP_ZONES = 256
# Shock tube to solve
$SHOCK_TUBE = "SOD"
# adiabatic index
$GAS_GAMMA = 5.0/3.0
# Atmospheric Pressure
$REFERENCE_PRESSURE = 1.0 # [Pa]
# density of air
$REFERENCE_DENSITY = 1.0 # [kg/m^3]
# end time for simulation (units of # of sound wave crossings)
$TEND = 0.125
# number of frames
$NUMDUMPS = 10
# Whether to use a diffusive (but robust) integration scheme
$DIFFUSIVE = False
# Order in time
$TIME_ORDER = "second"
# Write data for restarting the simulation
$WRITE_RESTART = False
# Output info for debugging purposes
$DEBUG = False
# Default dimensionality
$NDIM = 1

# nominal speed of sound
$ c0 = math.sqrt(GAS_GAMMA*REFERENCE_PRESSURE/REFERENCE_DENSITY) # [m/s]

# Set end time according to (user specified)
# number of times a wave crosses the box.
$END_TIME = $PERP_LENGTH*TEND/c0$

$XMIN = -0.5*PERP_LENGTH
$XMAX =  0.5*PERP_LENGTH
$YMIN = -0.5*PAR_LENGTH
$YMAX =  0.5*PAR_LENGTH
$ZMIN = -0.5*PAR_LENGTH
$ZMAX =  0.5*PAR_LENGTH

$if NDIM==1
$ CFL = 0.5
$ numCells = [PERP_ZONES]
$ periodicDirections = []
$ lowerBounds = [XMIN]
$ upperBounds = [XMAX]
$ else
$if NDIM==2
$ CFL = 0.4
$ numCells = [PERP_ZONES, PAR_ZONES]
# Make the direction perpendicular to the shock
# normal periodic.
$ periodicDirections = [1]
$ lowerBounds = [XMIN,  YMIN]
$ upperBounds = [XMAX,  YMAX]
$ else
$ CFL = 0.32
$ numCells = [PERP_ZONES, PAR_ZONES, PAR_ZONES]
# Make the directions perpendicular to the shock
# normal periodic.
$ periodicDirections = [1,2]
$ lowerBounds = [XMIN,  YMIN,  ZMIN]
$ upperBounds = [XMAX,  YMAX,  ZMAX]
$ endif
$ endif

# Initialize a USim simulation
initializeFluidSimulation(NDIM,0.0,END_TIME,NUMDUMPS,CFL,GAS_GAMMA,WRITE_RESTART,DEBUG)

# Setup the grid
addGrid(lowerBounds, upperBounds, numCells, periodicDirections)

Creating a Fluid Simulation

The next step in setting up a USim simulation is to create the basic set of variables needed to simulate the fluid. This is accomplished through the createFluidSimulation macro, documented at Euler Macro:

createFluidSimulation()

Now that these variables have been automatically created via the macro, it is possible to specify the distribution of fluid on the grid. This is a three-step process:

  1. Use addVariable to add variables that are independent of grid position.
  2. Use addPreExpression to add quantities that are functions of grid position, variables and any previously defined PreExpression in this block. Evaluated before expressions and the result is not accessible outside of this block. Any number of PreExpressions can be added.
  3. Use addExpression to define each initial condition for the fluid. There is one expression for density, each component of momentum and the total energy. The order of the exprssions correspond to the order in the state vector and there can only be one expression per entry in the state vector.

For the ShockTube example, the variables added in Step 1 in the above process are:

addVariable(pi_value,math.pi)
addVariable(gas_gamma,GAS_GAMMA)
addVariable(densityL,DENSITY_L)
addVariable(densityR,DENSITY_R)
addVariable(pressureL,PRESSURE_L)
addVariable(pressureR,PRESSURE_R)
addVariable(normalVelocityL,NORMAL_VELOCITY_L)
addVariable(normalVelocityR,NORMAL_VELOCITY_R)
addVariable(perpendicularVelocityL,PERPENDICULAR_VELOCITY_L)
addVariable(perpendicularVelocityR,PERPENDICULAR_VELOCITY_R)
addVariable(tangentialVelocityL,TANGENTIAL_VELOCITY_L)
addVariable(tangentialVelocityR,TANGENTIAL_VELOCITY_R)

The variables are then used in the PreExpressions that are defined in Step 2:

addPreExpression(rho = if (x>0.0, densityR,               densityL))
addPreExpression(pr  = if (x>0.0, pressureR,              pressureL))
addPreExpression(vx  = if (x>0.0, normalVelocityR,        normalVelocityL))
addPreExpression(vy  = if (x>0.0, perpendicularVelocityR, perpendicularVelocityL))
addPreExpression(vz  = if (x>0.0, tangentialVelocityR,    tangentialVelocityL))

Finally, these PreExpressions are used to specify the initial conditions define in Step 3:

addExpression(rho)
addExpression(rho*vx)
addExpression(rho*vy)
addExpression(rho*vz)
addExpression((pr/(gas_gamma-1))+0.5*rho*(vx*vx+vy*vy+vz*vz))

The ShockTube example includes many different initial conditions that are based on a range of cases proposed in the literature. The simples case is the SOD shock tube, specified through $SHOCK_TUBE = “SOD” above. This corresponds to the following variable definitions:

$ DENSITY_L = $3.0*REFERENCE_DENSITY$
$ DENSITY_R = $0.125*REFERENCE_DENSITY$
$ PRESSURE_L = $1.0*REFERENCE_PRESSURE$
$ PRESSURE_R =  $0.1*REFERENCE_PRESSURE$
$ NORMAL_VELOCITY_L = 0.0
$ NORMAL_VELOCITY_R = 0.0
$ PERPENDICULAR_VELOCITY_L = 0.0
$ PERPENDICULAR_VELOCITY_R = 0.0
$ TANGENTIAL_VELOCITY_L = 0.0
$ TANGENTIAL_VELOCITY_R = 0.0

Our simulation now looks like:

# Import macros to setup simulation
$ import fluidsBase.mac
$ import euler.mac

# X-extent of domain
$PAR_LENGTH = 1.0
# Y-extent of domain
$PERP_LENGTH = 1.0
# Zones parallel to shock normal direction
$PAR_ZONES = 256
# Zones perpendicular to shock normal direction
$PERP_ZONES = 256
# Shock tube to solve
$SHOCK_TUBE = "SOD"
# adiabatic index
$GAS_GAMMA = 5.0/3.0
# Atmospheric Pressure
$REFERENCE_PRESSURE = 1.0 # [Pa]
# density of air
$REFERENCE_DENSITY = 1.0 # [kg/m^3]
# end time for simulation (units of # of sound wave crossings)
$TEND = 0.125
# number of frames
$NUMDUMPS = 10
# Whether to use a diffusive (but robust) integration scheme
$DIFFUSIVE = False
# Order in time
$TIME_ORDER = "second"
# Write data for restarting the simulation
$WRITE_RESTART = False
# Output info for debugging purposes
$DEBUG = False
# Default dimensionality
$NDIM = 1

# nominal speed of sound
$ c0 = math.sqrt(GAS_GAMMA*REFERENCE_PRESSURE/REFERENCE_DENSITY) # [m/s]

# Set end time according to (user specified)
# number of times a wave crosses the box.
$END_TIME = $PERP_LENGTH*TEND/c0$

$XMIN = -0.5*PERP_LENGTH
$XMAX =  0.5*PERP_LENGTH
$YMIN = -0.5*PAR_LENGTH
$YMAX =  0.5*PAR_LENGTH
$ZMIN = -0.5*PAR_LENGTH
$ZMAX =  0.5*PAR_LENGTH

$if NDIM==1
$ CFL = 0.5
$ numCells = [PERP_ZONES]
$ periodicDirections = []
$ lowerBounds = [XMIN]
$ upperBounds = [XMAX]
$ else
$if NDIM==2
$ CFL = 0.4
$ numCells = [PERP_ZONES, PAR_ZONES]
# Make the direction perpendicular to the shock
# normal periodic.
$ periodicDirections = [1]
$ lowerBounds = [XMIN,  YMIN]
$ upperBounds = [XMAX,  YMAX]
$ else
$ CFL = 0.32
$ numCells = [PERP_ZONES, PAR_ZONES, PAR_ZONES]
# Make the directions perpendicular to the shock
# normal periodic.
$ periodicDirections = [1,2]
$ lowerBounds = [XMIN,  YMIN,  ZMIN]
$ upperBounds = [XMAX,  YMAX,  ZMAX]
$ endif
$ endif

# Parameters to specify the fluid state at t=0.0
$ DENSITY_L = $3.0*REFERENCE_DENSITY$
$ DENSITY_R = $0.125*REFERENCE_DENSITY$
$ PRESSURE_L = $1.0*REFERENCE_PRESSURE$
$ PRESSURE_R =  $0.1*REFERENCE_PRESSURE$
$ NORMAL_VELOCITY_L = 0.0
$ NORMAL_VELOCITY_R = 0.0
$ PERPENDICULAR_VELOCITY_L = 0.0
$ PERPENDICULAR_VELOCITY_R = 0.0
$ TANGENTIAL_VELOCITY_L = 0.0
$ TANGENTIAL_VELOCITY_R = 0.0

# Initialize a USim simulation
initializeFluidSimulation(NDIM,0.0,END_TIME,NUMDUMPS,CFL,GAS_GAMMA,WRITE_RESTART,DEBUG)

# Setup the grid
addGrid(lowerBounds, upperBounds, numCells, periodicDirections)

# Create data structures needed for the simulation
createFluidSimulation()

# Step 1: Add Variables
addVariable(pi_value,math.pi)
addVariable(gas_gamma,GAS_GAMMA)
addVariable(densityL,DENSITY_L)
addVariable(densityR,DENSITY_R)
addVariable(pressureL,PRESSURE_L)
addVariable(pressureR,PRESSURE_R)
addVariable(normalVelocityL,NORMAL_VELOCITY_L)
addVariable(normalVelocityR,NORMAL_VELOCITY_R)
addVariable(perpendicularVelocityL,PERPENDICULAR_VELOCITY_L)
addVariable(perpendicularVelocityR,PERPENDICULAR_VELOCITY_R)
addVariable(tangentialVelocityL,TANGENTIAL_VELOCITY_L)
addVariable(tangentialVelocityR,TANGENTIAL_VELOCITY_R)

# Step 2: Add Pre-Expressions
addPreExpression(rho = if (x>0.0, densityR,               densityL))
addPreExpression(pr  = if (x>0.0, pressureR,              pressureL))
addPreExpression(vx  = if (x>0.0, normalVelocityR,        normalVelocityL))
addPreExpression(vy  = if (x>0.0, perpendicularVelocityR, perpendicularVelocityL))
addPreExpression(vz  = if (x>0.0, tangentialVelocityR, tangentialVelocityL))

# Step 3: Add expressions specifying initial condition on density,
# momentum, total energy
addExpression(rho)
addExpression(rho*vx)
addExpression(rho*vy)
addExpression(rho*vz)
addExpression((pr/(gas_gamma-1))+0.5*rho*(vx*vx+vy*vy+vz*vz))

Evolving the Fluid

USim implements the well-known MUSCL scheme to advance the conserved variables in time. There is a simple macro that can be called to implement this scheme as shown below:

finiteVolumeScheme(DIFFUSIVE)

This macro is documented at Euler Macro. It’s purpose is to compute the numerical flux for the hyperbolic system:

\[\notag \begin{align} \nabla\cdot\left[ \mathcal{F} \left( \mathbf{w} \right) \right] - \mathcal{S} \left( \mathbf{w} \right) \end{align}\]

The next part of evolving the fluid is to apply boundary conditions at the left and right of the domain to ensure that at the next time step, physically-valid data is used to update the conserved state. Without this, the simulation will fail. It is possible to specify arbitrary boundary conditions in USim. For the Sod shock tube example considered here, appropriate boundary conditions are outflow (“open”) boundary conditions at both ends of the domain

boundaryCondition(copy,left)
boundaryCondition(copy,right)

The copy boundary condition block is described in copy (1d, 2d, 3d). This boundary condition updater copies the values on the layer next to the ghost cells into the ghost cells - this is equivalent to a zero derivative boundary condition. If we are evolving in more than one-dimension, we have to specify boundary conditions on the rest of the domain boundaries. For this example, this is done using periodic boundary conditions (periodicCartBc (1d, 2d, 3d)):

boundaryCondition(periodic)

The final element of advancing the conserved quantities from time \(t\) to \(t+\Delta t\) is to apply a time integration scheme, specified through:

timeAdvance(TIME_ORDER)

This applies an explicit Runge-Kutta time-integration scheme with the order of accuracy determined by the TIME_ORDER parameter. TIME_ORDER can be one of first, second, third or fourth according to the desired order of accuracy.

Putting it all Together

The final step in the USim simulation is to add:

runFluidSimulation()

This tells USim that we’re done specifying the simulation and that it can be run. So, our simulation now looks like:

# Import macros to setup simulation
$ import fluidsBase.mac
$ import euler.mac

# X-extent of domain
$PAR_LENGTH = 1.0
# Y-extent of domain
$PERP_LENGTH = 1.0
# Zones parallel to shock normal direction
$PAR_ZONES = 256
# Zones perpendicular to shock normal direction
$PERP_ZONES = 256
# Shock tube to solve
$SHOCK_TUBE = "SOD"
# adiabatic index
$GAS_GAMMA = 5.0/3.0
# Atmospheric Pressure
$REFERENCE_PRESSURE = 1.0 # [Pa]
# density of air
$REFERENCE_DENSITY = 1.0 # [kg/m^3]
# end time for simulation (units of # of sound wave crossings)
$TEND = 0.125
# number of frames
$NUMDUMPS = 10
# Whether to use a diffusive (but robust) integration scheme
$DIFFUSIVE = False
# Order in time
$TIME_ORDER = "second"
# Write data for restarting the simulation
$WRITE_RESTART = False
# Output info for debugging purposes
$DEBUG = False
# Default dimensionality
$NDIM = 1

# nominal speed of sound
$ c0 = math.sqrt(GAS_GAMMA*REFERENCE_PRESSURE/REFERENCE_DENSITY) # [m/s]

# Set end time according to (user specified)
# number of times a wave crosses the box.
$END_TIME = $PERP_LENGTH*TEND/c0$

$XMIN = -0.5*PERP_LENGTH
$XMAX =  0.5*PERP_LENGTH
$YMIN = -0.5*PAR_LENGTH
$YMAX =  0.5*PAR_LENGTH
$ZMIN = -0.5*PAR_LENGTH
$ZMAX =  0.5*PAR_LENGTH

$if NDIM==1
$ CFL = 0.5
$ numCells = [PERP_ZONES]
$ periodicDirections = []
$ lowerBounds = [XMIN]
$ upperBounds = [XMAX]
$ else
$if NDIM==2
$ CFL = 0.4
$ numCells = [PERP_ZONES, PAR_ZONES]
# Make the direction perpendicular to the shock
# normal periodic.
$ periodicDirections = [1]
$ lowerBounds = [XMIN,  YMIN]
$ upperBounds = [XMAX,  YMAX]
$ else
$ CFL = 0.32
$ numCells = [PERP_ZONES, PAR_ZONES, PAR_ZONES]
# Make the directions perpendicular to the shock
# normal periodic.
$ periodicDirections = [1,2]
$ lowerBounds = [XMIN,  YMIN,  ZMIN]
$ upperBounds = [XMAX,  YMAX,  ZMAX]
$ endif
$ endif

# Parameters to specify the fluid state at t=0.0
$ DENSITY_L = $3.0*REFERENCE_DENSITY$
$ DENSITY_R = $0.125*REFERENCE_DENSITY$
$ PRESSURE_L = $1.0*REFERENCE_PRESSURE$
$ PRESSURE_R =  $0.1*REFERENCE_PRESSURE$
$ NORMAL_VELOCITY_L = 0.0
$ NORMAL_VELOCITY_R = 0.0
$ PERPENDICULAR_VELOCITY_L = 0.0
$ PERPENDICULAR_VELOCITY_R = 0.0
$ TANGENTIAL_VELOCITY_L = 0.0
$ TANGENTIAL_VELOCITY_R = 0.0

# Initialize a USim simulation
initializeFluidSimulation(NDIM,0.0,END_TIME,NUMDUMPS,CFL,GAS_GAMMA,WRITE_RESTART,DEBUG)

# Setup the grid
addGrid(lowerBounds, upperBounds, numCells, periodicDirections)

# Create data structures needed for the simulation
createFluidSimulation()

# Step 1: Add Variables
addVariable(pi_value,math.pi)
addVariable(gas_gamma,GAS_GAMMA)
addVariable(densityL,DENSITY_L)
addVariable(densityR,DENSITY_R)
addVariable(pressureL,PRESSURE_L)
addVariable(pressureR,PRESSURE_R)
addVariable(normalVelocityL,NORMAL_VELOCITY_L)
addVariable(normalVelocityR,NORMAL_VELOCITY_R)
addVariable(perpendicularVelocityL,PERPENDICULAR_VELOCITY_L)
addVariable(perpendicularVelocityR,PERPENDICULAR_VELOCITY_R)
addVariable(tangentialVelocityL,TANGENTIAL_VELOCITY_L)
addVariable(tangentialVelocityR,TANGENTIAL_VELOCITY_R)

# Step 2: Add Pre-Expressions
addPreExpression(rho = if (x>0.0, densityR,               densityL))
addPreExpression(pr  = if (x>0.0, pressureR,              pressureL))
addPreExpression(vx  = if (x>0.0, normalVelocityR,        normalVelocityL))
addPreExpression(vy  = if (x>0.0, perpendicularVelocityR, perpendicularVelocityL))
addPreExpression(vz  = if (x>0.0, tangentialVelocityR, tangentialVelocityL))

# Step 3: Add expressions specifying initial condition on density,
# momentum, total energy
addExpression(rho)
addExpression(rho*vx)
addExpression(rho*vy)
addExpression(rho*vz)
addExpression((pr/(gas_gamma-1))+0.5*rho*(vx*vx+vy*vy+vz*vz))

# Add the spatial discretization of the fluxes
finiteVolumeScheme(DIFFUSIVE)

# Boundary conditions
boundaryCondition(copy,left)
boundaryCondition(copy,right)
boundaryCondition(periodic)

# Time integration
timeAdvance(TIME_ORDER)

# Run the simulation!
runFluidSimulation()

Note

For more depth, you can view the actual input blocks to Ulixes in the Setup window by choosing Save And Process Setup and then clicking on the shockTube.in file. In the .in file all macros are expanded to produce input blocks.

Most USimBase simulations have a underlying pattern, that can be represented as:

# Import macros to setup simulation
$ import fluidsBase.mac
$ import euler.mac

# Specify parameters for the specific physics problem
$ PARAM_1 = <value>
$ PARAM_2 = <value>
$ PARAM_N = <value>

# Initialize a USim simulation
initializeFluidSimulation(NDIM,0.0,END_TIME,NUMDUMPS,CFL,GAS_GAMMA,WRITE_RESTART,DEBUG)

# Setup the grid
addGrid(lowerBounds, upperBounds, numCells, periodicDirections)

# Create data structures needed for the simulation
createFluidSimulation()

# Specify initial condition
# Step 1: Add Variables
addVariable(NAME,<value>)

# Step 2: Add Pre-Expressions
addPreExpression(<PreExpression>)

# Step 3: Add expressions specifying initial condition on density,
# momentum, total energy
addExpression(<expression>)

# Add the spatial discretization of the fluxes
finiteVolumeScheme(DIFFUSIVE)

# Boundary conditions
boundaryCondition(<boundaryCondition,entity>)

# Time integration
timeAdvance(TIME_ORDER)

# Run the simulation!
runFluidSimulation()

We will see this pattern repeated through USimBase.

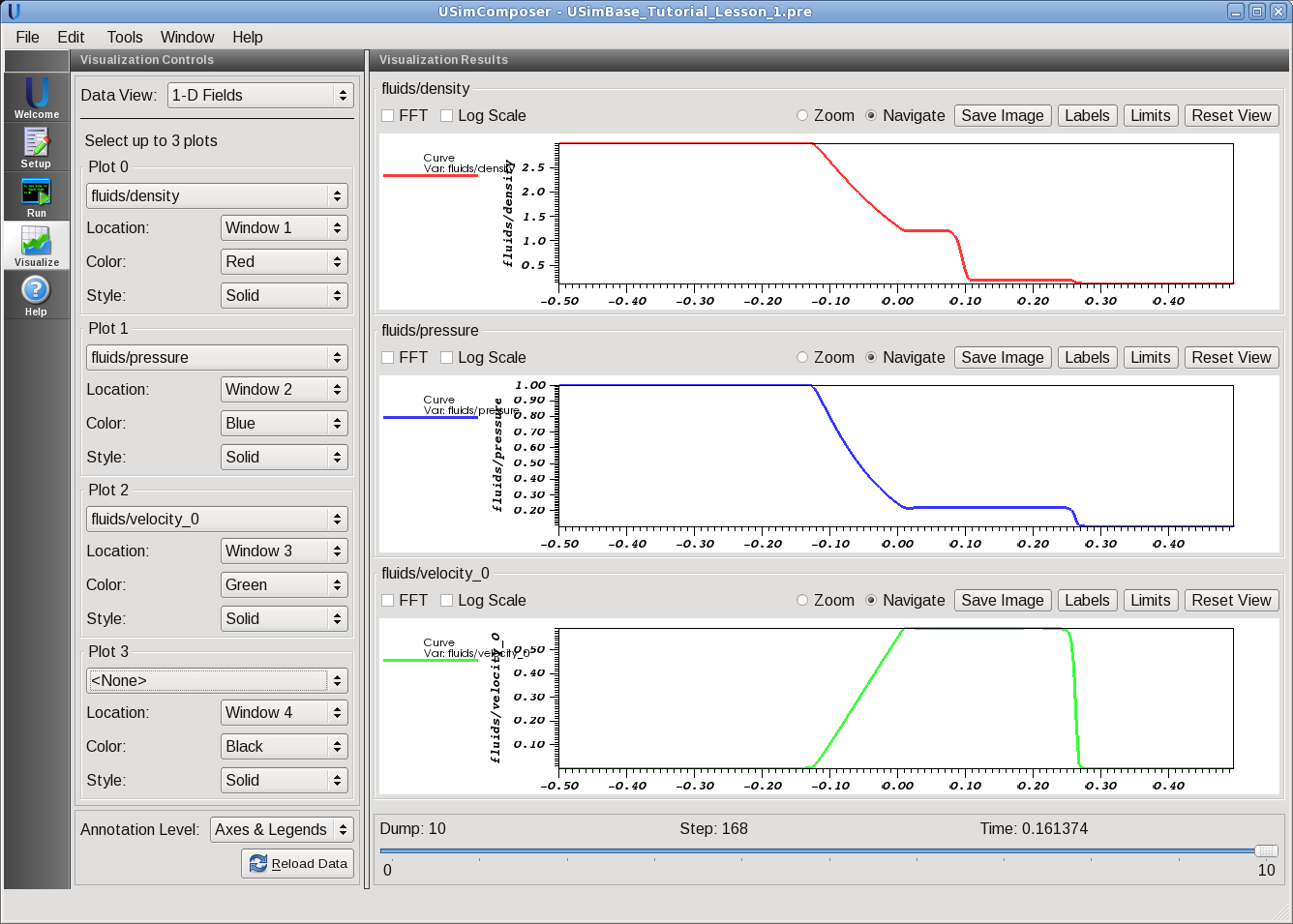
An Example Simulation

The input file for the problem Shock Tube in the USimBase package demonstrates each of the concepts described above to evolve the classic Sod Shock tube problem in one-dimensional hydrodynamics. Executing this input file within USimComposer and switching to the Visualize tab yields the plots shown in Fig. 1.

image 1

Figure 1: Visualization tab in USimComposer after executing the input file for this lesson.