Townsend Discharge (townsend.sdf)
Keywords:
- background gas, particle emission, ionization, inelastic anisotropic scattering
Problem Description
In a Townsend avalanche, electrons are accelerated by an electric field and ionize a background gas of neutral atoms or molecules. Each ionization event creates an additional electron that will also be accelerated and eventually produce more ionization events of its own. This process of repeated doubling results in an exponential increase in the number of electrons. The Townsend avalanche occurs when the electron and ion densities are too low to behave collectively and form a plasma.
This type of discharge is named after John Townsend who first proposed (c. 1897) the ionization model to explain the phenomena. In his experiments, Townsend measured the current across a gas-filled chamber with a pair of parallel plates on the two ends. Townsend illuminated the cathode plate with X-rays which produced electrons via the photo-electric effect. Townsend noticed that the current between the plates depended on the strength of the electric field between the plates and the pressure of the gas.
His observations lead to the conclusion that electrons were ionizing the gas and causing an exponential increase in the measured current. The current measured across the discharge chamber is described by the following formula:
where \(I_0\) is the photo-current produced by the X-rays, \(I(x)\) is the current through the chamber as a function of the plate separation, \(x\). The parameter \(x_0\) is a characteristic distance that a collection of electrons has to travel away from the cathode before an equilibrium is reached. The parameters \(\alpha\) and \(\gamma\) are the first and second Townsend coefficients, respectively. The first Townsend coefficient, \(\alpha\) is a measure of how many ionization events a single electron will produce per unit length, and \(\gamma\) is a parameter accounting for electron generation from secondary processes, like ion impact at the cathode.
In this example simulation, we will loosely follow the experimental setup of L.M. Chanin and G.D. Rork who measured the first Townsend coefficient for Helium [CR64a], Neon, and Hydrogen [CR64b] in the 1960s. For low voltage discharges, the factor \(\gamma\) is negligible and the equation above reduces to:
In reality, \(\alpha\) is a complicated function of pressure, accelerating field, and the species of background gas molecule/atom. Chapter 14 section 3 of Principles of Plasma Discharges and Materials Processing, [LL05] presents an analytical model for \(\alpha\) as a function of pressure and electric field and provides the fitting constants for different gases. This simulation will estimate a value for \(\alpha\) for a Helium gas keeping the electric field and pressure constant at \(E = 2.12e5\) V/m and \(p = 21.2\) torr. It should be noted that Chanin and Rork [CR64a] measure to find \(\alpha / p_0\), rather than \(\alpha\) directly. At this pressure and electric field, the accepted value for \(\alpha / p_0\) is 1.3 [CR64a], [LL05].
This simulation can be run with a VSimPD license.
Opening the Simulation
The Townsend Avalanche example is accessed from within VSimComposer by the following actions:
Select the New → From Example… menu item in the File menu.
In the resulting Examples window expand the VSim for Plasma Discharges option.
Expand the Processes option.
Select Townsend Avalanche and press the Choose button.
In the resulting dialog box, create a New Folder if desired, then press the Save button to create a copy of this example.
The resulting Setup Window is shown Fig. 582.
Fig. 582 Setup Window for the Townsend Avalanche example.
Simulation Properties
In order to calculate a value for the Townsend coefficient, this simulation will need to be run multiple times at different plate separations while keeping the electric field and pressure constant. This parameter scan of plate separations can be done within the Design Tab, which is explained in Parameter Scan.
The data points from these multiple runs will be used in a least squares fit to an exponential function of the form:
where \(\alpha\) and \(\beta\) are the constants being fitted, with \(\alpha\) being the Townsend coefficient of interest. Details on how to fit the data yourself is covered in the section Computing the Townsend Coefficient below.
The simulation input file is set up to allow for rapid iteration on the multiple plate separations. The voltageDifference actually controls the separation of the two plates in such a way that keeps the electric field constant; it is also used to calculate an estimate for the maximum electron speed which goes into determining the time step.
In Basic Settings the field solver is set to prescribed fields. This
means we manually set the electric field as a function of space (and have an
option to add time dependence). In the Field Dynamics element, under
Fields is where we actually set the value for the constant electric field
present between the two plates at either end of the discharge tube. In the
externalElectricField element we set component0, the x-component of the
electric field to a value calculated from the parameters in
[CR64a].
The Particle Dynamics element is where we set up the which particle species the simulation will contain, how particles of each species get added and removed from the simulation, and in what processes/interactions they participate.
This simulation contains an electron species, a positive helium ion species,
and a background gas of helium neutral gas.
The settableFluxSlabElectronEmitterCW0 is set up to emit a total of
100,000 physical electrons. Both the electron and helium ion species have
been set up such that each macro particle corresponds to a single physical
particle.
The electric field points from upper x (right side of screen) to lower x
(left side of screen). The electrons are emitted into the simulation from
the lower x and are accelerated to the right. There are seven interactions
in which an electron can be involved as it crosses the simulation grid.
These processes are set in the Reactions element, which has been enabled
by choosing include particles and reactions in Basic Settings.
The processes included in this simulation are electron/neutral helium
elastic scattering, five different electron/neutral helium excitation
processes in which electrons lose some energy to putting a neutral helium
atom into an excited state, and an electron/neutral helium ionization process
which is the crucial bit of physics for this simulation.
We found that the it was important to use the reaction type
Inelastic Electron Scattering with scatter type set
to VahediSurendra for getting an accurate value for the Townsend coefficient.
To add collision processes to VSim, cross-sections data must be supplied by the user. To get the most accurate results from this validation study, we used cross sections from the LXCat database. According to the terms of the database, we are not permitted to distribute data obtained from the database, so the data included as part of this example is less accurate. Obtaining Cross-sections from LXCat contains a set of instructions for obtaining the more accurate cross-section data for yourself.
Running the Simulation
If the user would like to do a single run of the simulation:
Proceed to the run window by pressing the Run button in the left column of buttons.
Here you can set run parameters, including how many cores to run with (under the MPI tab).
When you are finished setting run parameters, click on the Run button in the upper left corner. You will see the output of the run in the right pane. The run has completed when you see the output, “Engine completed successfully.” This is shown in Fig. 583.
Fig. 583 The Run window at the end of execution.
Parameter Scan
In order to start a parameter scan
Proceed to the design window by pressing the Design button in the left column of buttons.
The left sub-panel, Runtime Options, of the Design window contains several sub-elements
Within the Setup sub-element we can edit the Scan Name and we can Add Parameter(s) to iterate over.
Here we are iterating over the constant voltageDifference
The Model Choice drop-down menu has two options: List and Range.
For the voltageDifference constant, the model choice has been set to List.
The list should have seven (7) values to scan over (40, 60, 80, 100, 120, 140, 160).
Below the Model Choice and options, is the Run Settings sub-element.
Here you can set the scan/run parameters, including how many cores to run with.
The Default settings is to do serial runs for each parameter choice with the max concurrent runs equal to the licensed number of cores.
When you are finished setting run parameters, click on the Run button in the upper left corner. You will see the output of the run in the right pane. The run has completed when you see the output, “Engine completed successfully.” This is shown in Fig. 584.
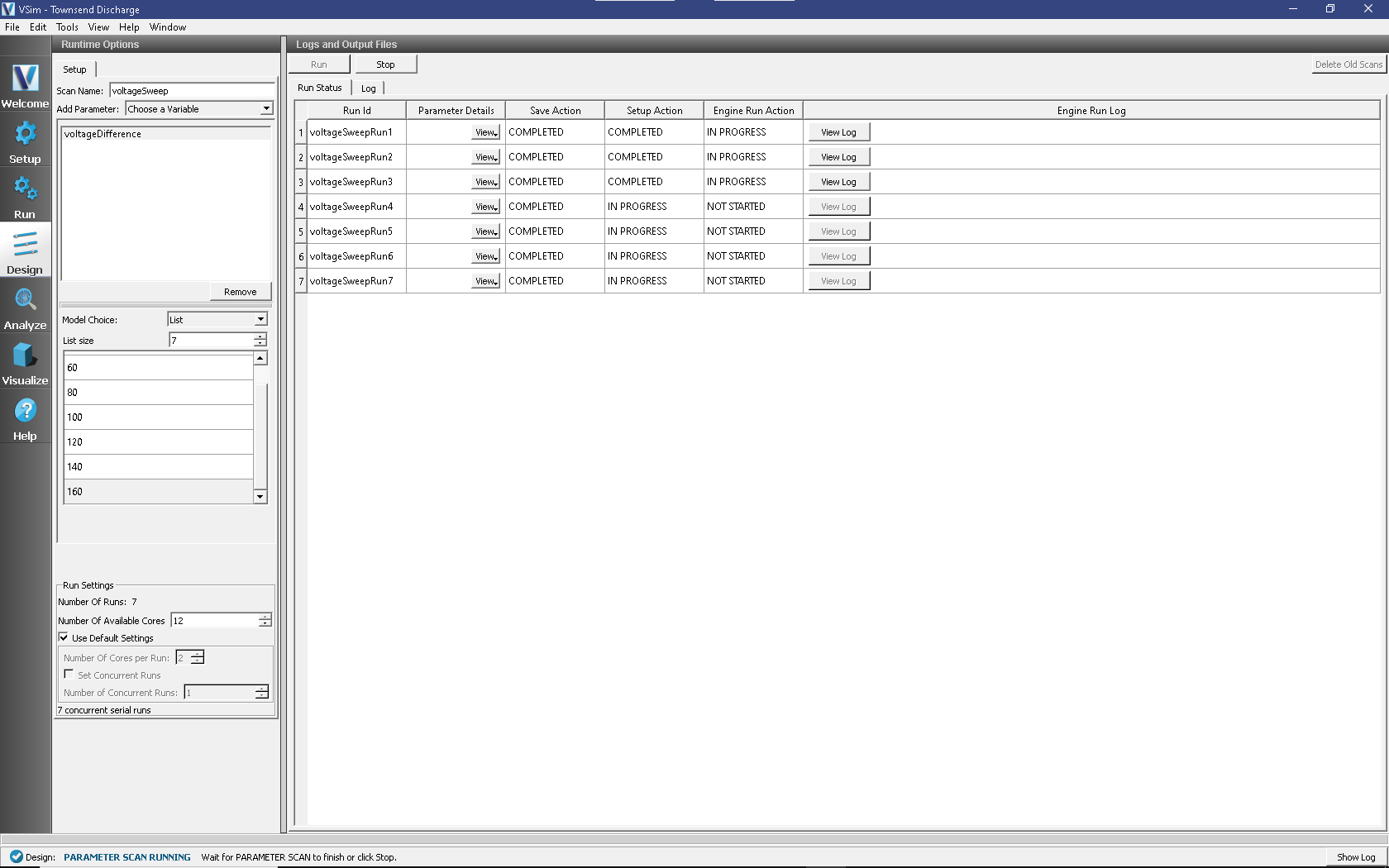
Fig. 584 The Design window at the end of execution.
Computing the Townsend Coefficient
To collect enough data and make a fit to
this simulation will need to be run multiple times with different plate separations. Since the electric field is constant, different plate separations correspond to different voltage differences between the right and left plates. As the plates get further apart, electrons will have more space to accelerate and ionize the neutral helium gas. Since the total number of helium ions created in collisions with electrons depends on the total number of electrons in the space between the two electrodes, the exponential form of the equation above is expected.
The Design Tab allows for easy modification of the the plate separation and running of multiple concurrent simulations.
If the user prefers to modify these values by hand:
To adjust the plate separation, change the voltageDifference constant which is under Constants in the setup tree. The simulation will open with this constant set to 40 volts. When we performed this study, we ran at voltages of 40, 60, 80, 100, 120, 140, and 160 volt differences.
Following the generation of this data for volt differences, we then ran scanAnalyzerTownsend.py which can extract the data from the simulation folders generated via a Scan. The scan analyzer will then produce \(\frac{\alpha}{p_0}\). as seen in Fig. 585.
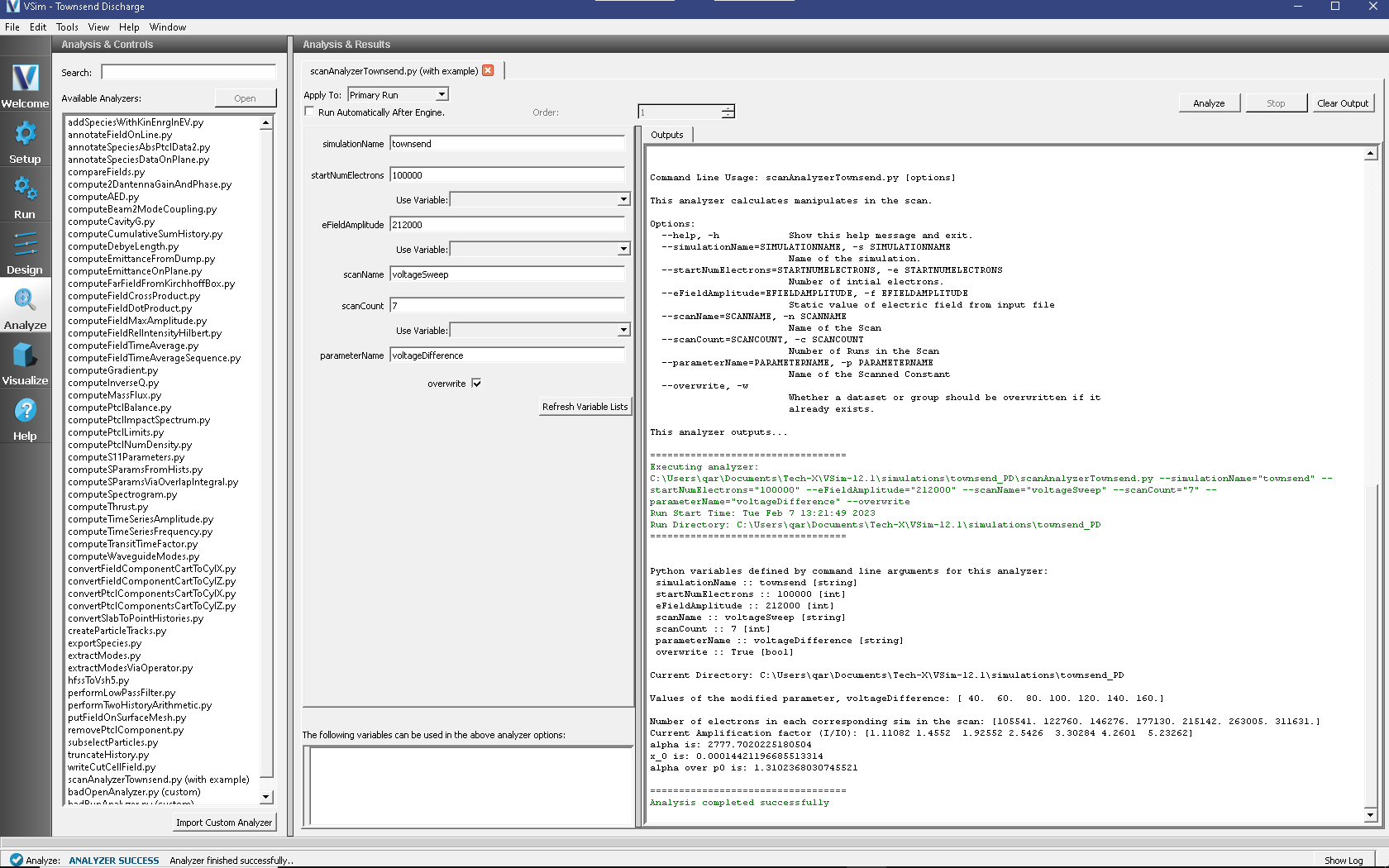
Fig. 585 The Analyzer window at the end of execution.
scanAnalyzerTownsend.py requires the scanName and the number of simulations run in the scan, along with some other values; it then computes the townsend coefficient. This is done by obtaining several values from each simulation:
The voltage difference between plates,
The electron current on the upper X absorber (i.e. downstream of the ionizing reactions).
The step size, dt
Using the electron current on the upperXAbsorber, dt, the initial number of electrons and the elemental charge, we can calculate the number of electrons that are produced. Note, we consider each particle to represent one “unit” of current, in that \(I_{unit} = Q_{elementary} / dt\).
The number of electrons produced is useful as we can then determine the current amplification factor associated with each voltage difference.
The analyzer then calculates \(\alpha\) and \(x_0\) from the separation between plates and the current amplification factor. It does so via statistical averages of those values in order to determine a slope and intercept, similar to \(y = m*x + b\). The slope, \(m\) is our \(\alpha\), while \(x_0\) is the negative of the intercept over the slope. The analyzer prints both \(\alpha\) and \(x_0\) before printing the value of interest, \(\frac{\alpha}{p_0}\). As a reminder to the reader, we are looking to compare to Chanin/Rorks’ \(\frac{\alpha}{p_0}\), as those are the experimentally provided values.
Further Experiments
Run the simulation at a different pressure to measure the Townsend coefficient in a different regime.
Change the gas type by switching the ion species, gas species, and cross-sections.